When: Thursday 17th of April, 1:00pm AEST
Where: This seminar will be partially presented at the ACFR seminar area, J04 lvl 2 (Rose St Building) and partially online via Zoom. RSVP
Speaker: Jing Cheng
Title: Learning Stable and Passive Neural Differential Equations (joint work with Ruigang Wang and Dechuan Liu)
Abstract:
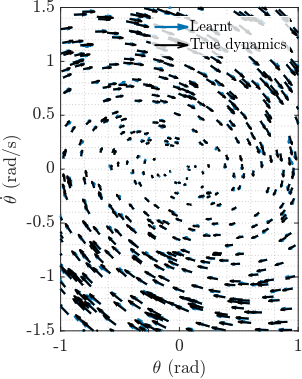
Ensuring certain stability guarantees in neural network models is now widely regarded as essential in machine learning and control community. In this talk, we introduce a novel class of neural differential equations, which can be intrinsically Lyapunov stable, exponentially stable or passive. We take a recently proposed Polyak Lojasiewicz network (PLNet) as an Lyapunov function and then parameterize the vector field as the descent directions of the Lyapunov function. The resulting models have a same structure as the general Hamiltonian dynamics, where the Hamiltonian is lower- and upper-bounded by quadratic functions. Moreover, it is also positive definite w.r.t. either a known or learnable equilibrium. We illustrate the effectiveness of the proposed model on a damped double pendulum system. We will also briefly discuss on some potential extensions from this work.
Bio:
Jing Cheng received his bachelor’s degree at Harbin Institute of Technology (HIT) in 2014 and master’s degree at the University of Sydney in 2018. Currently he is a PhD candidate at Australian Centre for Field Robotics (ACFR), working on force control and robust learning on surgical robots. His research interest includes robust machine learning and non-linear control.
